在学习线性代数的过程中常常遇到矩阵分解这个概念,从名字来看,大概就是A=PQ或者A=UVW这样的事情,但是,我们为什么要进行矩阵分解?各种矩阵分解具体是怎样实现的 ?种种问题始终困扰着我,这次我们来个大杂烩,深入理解矩阵分解的奥秘。
LU分解
说到最常见的矩阵分解,必然是LU分解,LU分解将满秩的方阵分解为一个下三角矩阵X一个上三角矩阵的形式,他在我么们进行高斯消元时就发挥了作用,具体是怎样实现的呢?
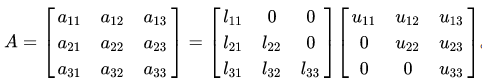
回忆高斯消元的过程,我们总是使用初等行变换,使用第一行消去其下面每行的第一列,使用第二行消去下面每行的第二列,最终的结果就是我们能得到一个上三角矩阵。需要注意的是过程中不能出现行交换的初等变换。
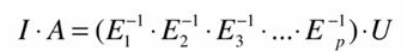
而大家又可得知,进行初等行变换,可以看做分解为左乘行变换矩阵的过程,而这些行变换矩阵的积总是一个下三角矩阵。
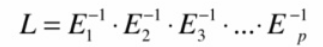
这样看下来,LU分解就是代表着高斯消元的过程。LU分解主要应用于求解线性方程Ax = b中,最容易想到的方法是求A的逆,但是这样费时费力,小学生最先想到的方法则是高斯消元,可以用LU分解的方式表示:
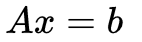
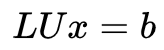
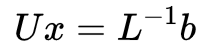
由于三角阵的逆很容易求得,我们很快就能求解x。
Cholesky分解
如果LU分解中的A矩阵同时也是一个对称正定矩阵的话,此时进行的LU分解也可看作是Cholesky分解。
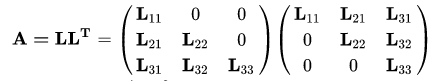
Cholesky分解类似于求解矩阵的平方根,在无迹卡尔曼滤波(UKF)中,求取Sigma点时使用的数值解方法就利用了Cholesky分解。
QR分解
相较于要求严格的LU分解,对于任意的方阵,我们都能对其进行QR分解,其可以将一个方阵分解为一个正交矩阵X一个上三角矩阵的形式。
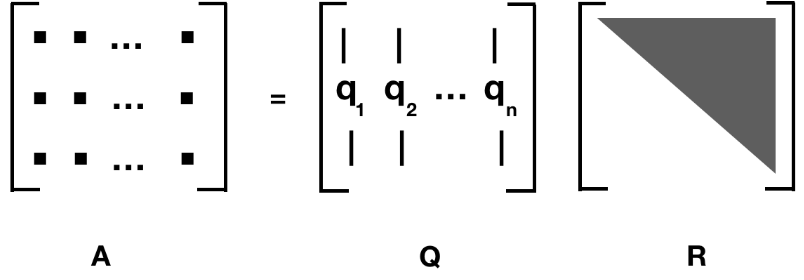
再让我们回忆一下Gram-Schmidt正交化。G-S正交化的作用是将原来表示子空间的基变为一组子空间的正交基来代表这个子空间,有了正交基,子空间中的向量就可以进一步使用正交坐标系统来表示了。G-S分解的过程非常简单就是不断地将下一个基减掉其在已经求得的正交基上的投影,得到的结果也就是在其他正交基方向上没有的部分,也就是新的正交基。
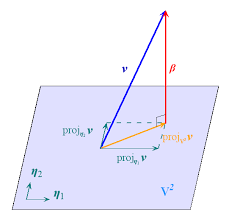
QR分解描述的就是这个过程:A中的列向量就是原本描述子空间的基,而结果中的Q即是描述子空间的新基,由于其正交的性质,Q也就成了一个正交矩阵,结果中的R代表着老基在新基中的坐标,由G-S正交化的过程可以看出,R可以表示为一个上三角矩阵。
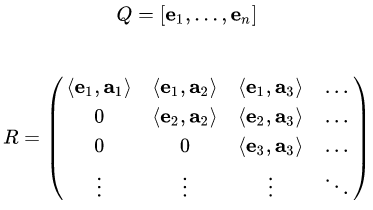
你有没有注意到上面所说的G-S分解是可以作用于子空间的,而我们说QR分解只能够作用于方阵,也就是这个子空间就是原空间本身!这样是不是限制了G-S分解的发挥呢?确实是如此,因此我们推广了QR分解,也就是广义的QR分解:
对于矩阵A(维度:mXn),若m > n,则可以将A矩阵的列向量看做是描述了一个m维空间中的n维子空间,这时我们同样能够对A进行G-S正交化,可以得到n个m维的正交基与n个n维的系数向量,这时的QR分解可以描述为:
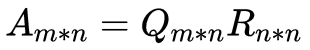
此时的R矩阵仍然是上三角矩阵,而Q则不再是正交矩阵了。但是我们可以使用脑补的方法帮助Q脑补一些正交的向量作为基,使得这组基能够描述整个空间,凑齐m个基,就能够将W矩阵脑补成一个正交矩阵了,只不过此时的R矩阵由于并没有利用到脑补出来的向量,则会产生数行全0的系数向量,这时的QR分解可以描述为:
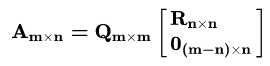
QR分解的应用也在于求解方程组Ax=b当中,只不过这次涉及到了子空间,所以这个方程组可能是一个超定的方程组,我们要利用上文提到的广义QR分解第二种形式,简化求解最小二乘问题,过程如下:
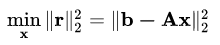
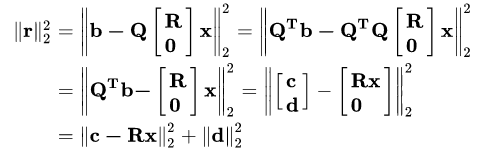
最后变为求解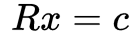 的问题,是一个全定的问题。
的问题,是一个全定的问题。
特征值分解(谱分解)
特征值大家都很熟悉,其实特征值分解大家也都有所了解,他的求解过程完全就是利用了特征值的定义:
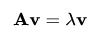
如果A是方阵(维度:nXn),且拥有n个线性无关的特征向量,则利用特征值与特征向量的定义,可以将其组合,整理为:
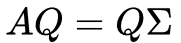
其中Q是特征向量作为列向量组合承德矩阵,由于特征向量线性无关,Q可逆的;Sigma是对应特征值构成的对角矩阵。最终特征值分解可表示为:
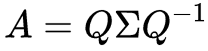
特征值分解的意义在于,它描述了矩阵A的基本性质。若将A视为一个线性变换矩阵,A的作用就是某个向量x变换为某个向量b,也就是Ax=b的过程。我们很难理解这个变换,但是我们可以使用特征值分解,将其拆分为:Q变换逆-Sigma变换-Q变换 的过程。其中Sigma描述了变换的缩放关系。特征值分解将一个复杂的变换描述为了两个简单的变换:一个坐标系的转换与一个缩放的变换。
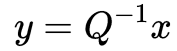
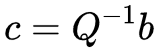
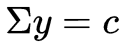
特别地,若A矩阵为实对称阵,则其不同特征值对应的特征向量互相正交,于是我们求得的Q矩阵变成了正交矩阵(描述一个旋转),对应的特征值分解也变成了:
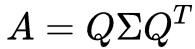
奇异值分解(SVD)
与特征值分解类似,奇异值分解也致力于寻找这样的描述变换本质的坐标变换+缩放,但是他所针对的目标在于描述任意矩阵而非仅针对于方阵。奇异值分解的形式为:
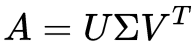
求解奇异值分解的方法很浅显易懂,既然方阵能够进行特征值分解,我们不如直接构造一个方阵,比如说,想要求解矩阵A(维度:mXn)的奇异值分解,我们构造:
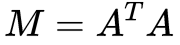
我们注意到这个M矩阵(维度:nXn)是一个对称阵,它的特征值分解会得到Q是一个nxn的正交矩阵,Sigma是一个nXn的对角矩阵,将奇异值分解的定义代入,可以得到:
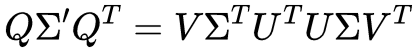
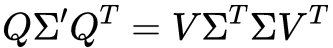
显而易见我们可以得到此时的Q即是奇异值分解中的V。同样的,计算AAT则可以得到U的值。Sigma的值也可以容易地求得。需要注意的是,Sigma是包含0行或0列的准对角矩阵,对角线元素是ATA或AAT特征值的根。
奇异值分解描述了任意一个矩阵的本质,他有很多的应用:
- 在PCA降维中,对矩阵A使用奇异值分解,去除结果中非主要元素的Sigma以及对应的U、V中的向量,仍能较好地还原矩阵A,此时奇异值分解描述的是矩阵元素的协方差。
- 在対极几何中,得到本质矩阵或基础矩阵,通常使用奇异值分解得到对应的R与t。
- ICP点云配准中也是用奇异值分解得到对应的R与t。