从刚上大学开始,积分变换就无时无刻地萦绕在我们身旁,什么傅里叶变换。拉普拉斯变换,甚至小波变换等等。
这些变换有什么意义?他们又是怎样实现的呢?这次我们多花点时间来理一理。
积分变换即基变换
就如同线性代数所说那样,空间中任意一个向量都可由一组完备(个数充满R^n)的正交的基的线性组合来表示。
如果把一个函数(信号)看作这个任意的向量(属于R^∞空间),那么这个函数也可以由R^∞空间下的一系列正交的基(也是函数、信号)来表示,这就是信号的基变换,也就是我们说的积分变换。这组正交基的选择,就是积分变换产生区别的地方,如何选择一组好用的基就成了我们要动脑筋的地方。
傅里叶、拉普拉斯等人选择到了一系列合适的正交基函数,使得进行基变换后表示的函数有着很好的性质(比如能量集中、方便微积分运算等等),于是成为了一系列经典的积分变换。由此我们看出,积分变换即基变换。
我们以傅里叶变换为例来进行研究
连续周期信号的变换
对于连续周期信号,傅里叶选择用一组正交函数基来表示他们,可以获得由时域转移到频域的优秀性质。这组基就是三角函数集(也可以用复指数集来表示)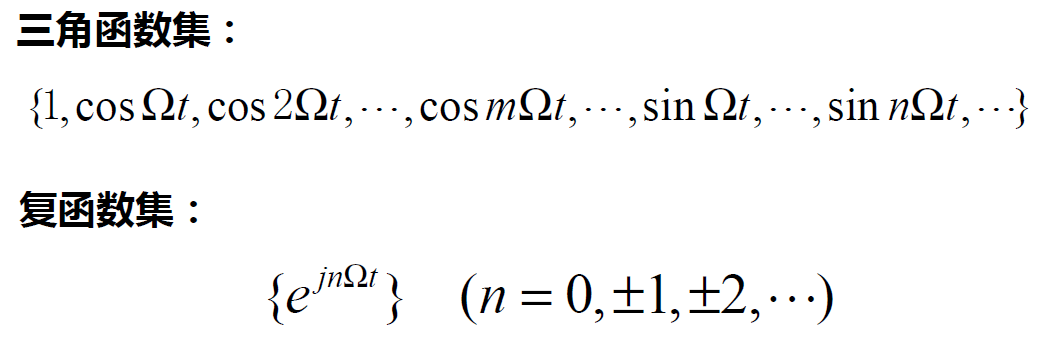
这样我们可以得到一组长度为无穷的级数,就是傅里叶级数。
注意到这里选择的基函数的频率为nω0,也就是原周期信号的整数倍,也就是说连续周期信号的频谱是离散的。
傅里叶级数这样来表示:
也可以表示成复指数形式: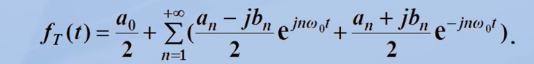
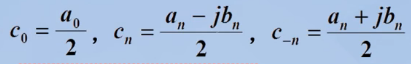
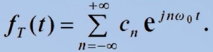
cn可通过基正交的性质求得: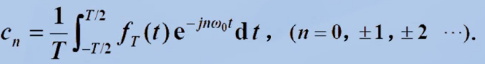
这个cn也就是输入函数的频谱,它的实数部分代表cos值,虚部代表sin值,也可以看作表示的是幅值与相位,如图: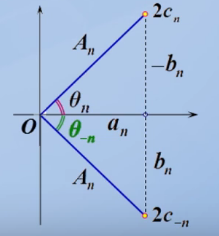
注!对于定义在有限区间的函数,将其进行周期延拓,也可将其看作周期信号,进行傅里叶级数展开。
看来基的选择还与原始信号有关,但当我输入一个非周期信号时,应该怎么选择这组基呢?
连续非周期信号的变换
对于非周期信号,我们可以把它看作一个周期->∞的信号,此时的ω0->0。
由于T->∞,Fn->0,不再适合描述频率特性,因此我们选择TFn = F(nω0)作为描述频率特性的函数.
这代表什么呢?这代表着非周期信号的频谱间隔很小,也就可以看作是连续的,此时nω0就退化成了ω,就与傅里叶变换如下:
同样刻画了输入信号的频率特性。
因此得到傅里叶变换与反变换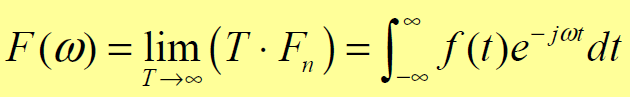
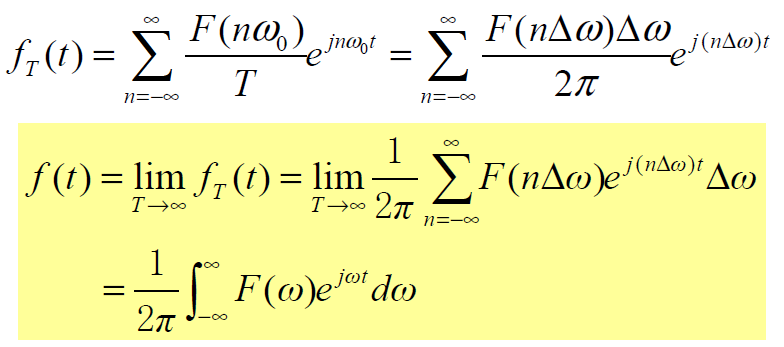
可以看出来,此时的F(ω)不再代表着频谱,而是表示频谱的密度。
也就是说,非周期函数不能表示成cos、sin的线性组合(由于系数->0),但是可以使用傅里叶变换衡量其中各个频率的成分多少。
离散非周期信号的变换
上述连续信号的傅里叶变换适用于模拟信号。随着数字控制的普及,我们如果想在一个离散的数字系统中进行傅里叶变换,必须进行离散的采样,采样可以用原信号*冲激序列来表示: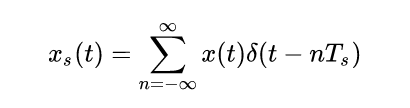
注意这个信号仍属于连续的信号,只不过他有了一个可以对应的离散序列也就是x[n]
我们当让可以对这个连续的信号进行连续的傅里叶变换: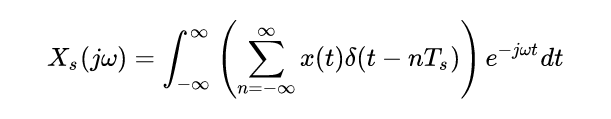
这里交换积分号与求和号,化简可以得到: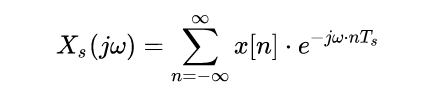
这里的离散序列x[n]就是由与之对应的冲激序列积分得来的,有x[n] = x(nTs)
这样一来我们就得到了离散信号的傅里叶变换,但是这个信号在频域上还是连续的,没办法用在数字处理器中:
一是因为这个求和是从-∞到+∞项的求和,需要知道信号时域的全部信息,这对于实时系统是不可能实现的;
二是由于频域上这个ω是连续的,也就是得到了频域上的全部信息(由于使用了信号时域的全部信息),离散系统ω是离散的,只能使用其中的一部分信息,造成了信息的冗余。
我们既然不能利用频域的全部信息,而却要求知道信号时域的全部信息,能否做一妥协,这时离散傅里叶变换出来救场了。
离散周期信号(有限长信号周期延拓)的变换
有限的时域信息表示有限的(离散的)频域信息,我们很自然地想到了周期函数的傅里叶级数。
同理,对于一个非无限长的信号(一张图片),或者是无限长信号的一段截取(实时数字系统本时刻的前N个采样周期信号的截取),我们可以对其进行延拓,这样就得到了一个无限长的周期信号。对这个周期信号进行傅里叶展开,就可以得到离散的频域表达了:
对这个离散的周期延拓进行傅里叶展开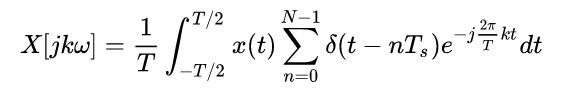
还是一样的计算方法,交换积分号与求和号,且有T = NTs,化简得到: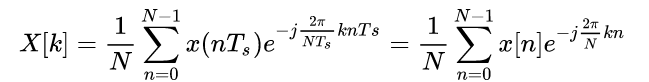
这就是N点离散傅里叶变换DFT的表达式,并且这个离散序列是以N为周期的,我们只取第一个周期即可。
其中第k个点表示的是kω0/N频率分量,其中ω0 = 1/Ts。
可以看出,这就是DTFT的离散化表示!
当然对于本来就是周期序列的信号,可以直接进行离散傅里叶级数展开DFS。
从上面的例子,我们看出,这种信息的守恒十分的美观:
时域的信息完备性体现在是否需要知道信号从出生到入死的全部(是否是周期的),而频域的信息完备性体现在频域表示是否是连续的。
或许这就是数学之美吧!!!!!
总结一下时域频域函数的对应关系:
- 时域连续->频域非周期
- 时域离散->频域周期
- 时域周期->频域离散
- 时域非周期->频域连续
是不是也很美呢?
二维离散信号(图片)的变换
待更新!