从去年这时候第一次从老余那儿听说到DR_CAN这个人,开始看他的视频,到现在,我已经把这部分内容反复看了4遍了,没有什么额外的原因,纯粹就是因为看不懂,看懂了就忘( ´・・)ノ(._.`),所以现在来这里总结一下!
这里超级感谢DR_CAN先生,这个up是真真正正的宝藏up,人帅,又有才华(特别推荐爱情中的数学这一期,老少皆宜),他也算是帮助我半只脚进入控制世界的大门的引路人吧ヾ(≧▽≦*)o

经典之作——love and math
这期内容分两篇文章,分别对应LTI与Non-Linear,期待期待!
状态方程与传递函数
学过经典控制理论的肯定对传递函数有所了解,传递函数描述了一个系统的性质,系统是否稳定,有没有震荡,收敛的快慢都可以由传递函数分析得出。
而在现代控制理论中,和传函同等地位的就数状态方程了,状态方程也可以描述这个系统。
状态方程的形式是这样的: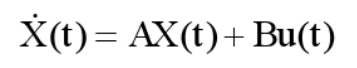
状态方程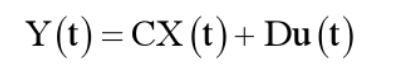
输出方程
其中,决定系统性质的,有着和传递函数分母相同作用的,就是A矩阵,它的特征值就是对应传函的极点,这条性质十分重要!
我们以二阶系统为例,若将X进行坐标变化,X=PY,使得Xdot=AX变换为Ydot=P^-1APY,使得P^(-1)AP为一个对角矩阵,这个对角矩阵的两个非零元素就是A的特征值,X变到Y,即完成了一个解耦,方便了我们分析,X,Y变化趋势相同,仅仅相差一个坐标变换,就像下面这样:
解耦后的系统相图一般有以下几种形式,对应不同的特征值: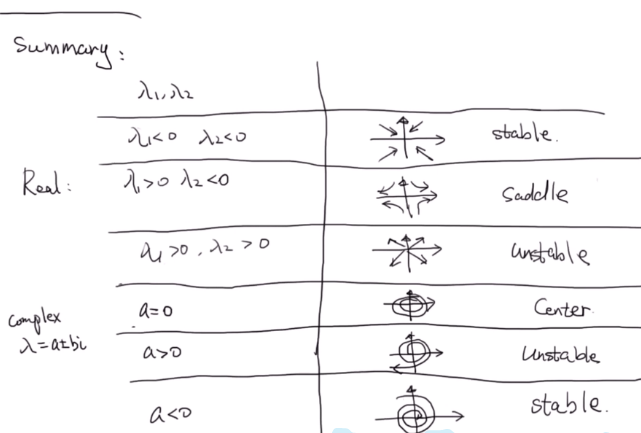
稳定性
在了解稳定性之前,我们先来理解一下平衡点的概念——
平衡点也是个很重要的概念:Xdot=0,即为平衡点,若系统初始在了平衡点,它的状态就永远不会变换,并且系统若是稳定,最终一定会趋近平衡点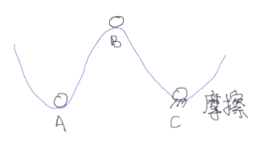
等幅振荡——不稳定——最终收敛的情况。
稳定性的数学定义如下:
第一种,也就是李雅普诺夫稳定(Lyapunov Stable),简单地理解就是将等幅振荡也算作稳定了,即最终x有界
第二种,也就是渐近稳定(Asymptotic Stable),简单地理解就是x最终必须收敛。
对于线性系统来讲,判断稳定性的方法很简单,就是观察A阵特征值的正负,全部小于等于0,则可以达到李雅普诺夫稳定,而若是全部小于0,则达到了渐近稳定的要求。
而对于非线性系统,就比较麻烦了,分为李雅普诺夫第一方法(解系统的微分方程,比较难)与李雅普诺夫第二方法(直接方法,通过寻找李雅普诺夫函数来判定),这方面我们将在下一篇中仔细理解。
可控性与控制器
上面我们讨论了在零输入的状态下,系统的稳定性,可见,对于任意的一个系统,稳定性是不能确定的,即使稳定,平衡点可能也不能满足我们的要求,于是我们就要加入控制变量来使得系统能够稳定,甚至能够改变系统的平衡点。
引入最简单的反馈控制器U = -kX,其中k = [k1,k2],这样我们新的系统就变成了Xdot=(A-Bk)X,我们就可以配置(A-Bk)的特征值,来计算k,使得新的系统满足我们的要求。
另外,控制器k的设计不仅能够由特征值配置(在经典理论中称为极点配置)得到,在最优控制(Optimal Control)中,考虑输入的情况下,通过使Cost Function最小而计算出k1、k2的值,我们称这种方法为LQR Control。
但是这样做有一个前提,即保证k有解,这就需要我们的系统满足可控性,系统具有可控性,就是系统状态变量在相平面上可以在输入的作用下达到任意的点,具体推导公式是DR_CAN用离散的方法推出来的,连续的方法我这里也不太会,希望知道的同学能来教教我,(≧∇≦)ノ
直接给出可控性的条件
当Co = [B AB A^2B ……A^nB]满秩时(即Rank = n时),即可证明k有解,也就是系统可控!
注意!!在相平面上,可控指的是点对点的可控,而不是轨迹上的可控!
可以控制系统稳定性之后,我们就想着要控制系统的轨迹,进行轨迹跟踪,也就是改变系统的平衡点!
引入误差变量e,有
e = x1d - x1
edot = x1ddot - x1dot
用新的状态变量e来表示系统方程则会得到: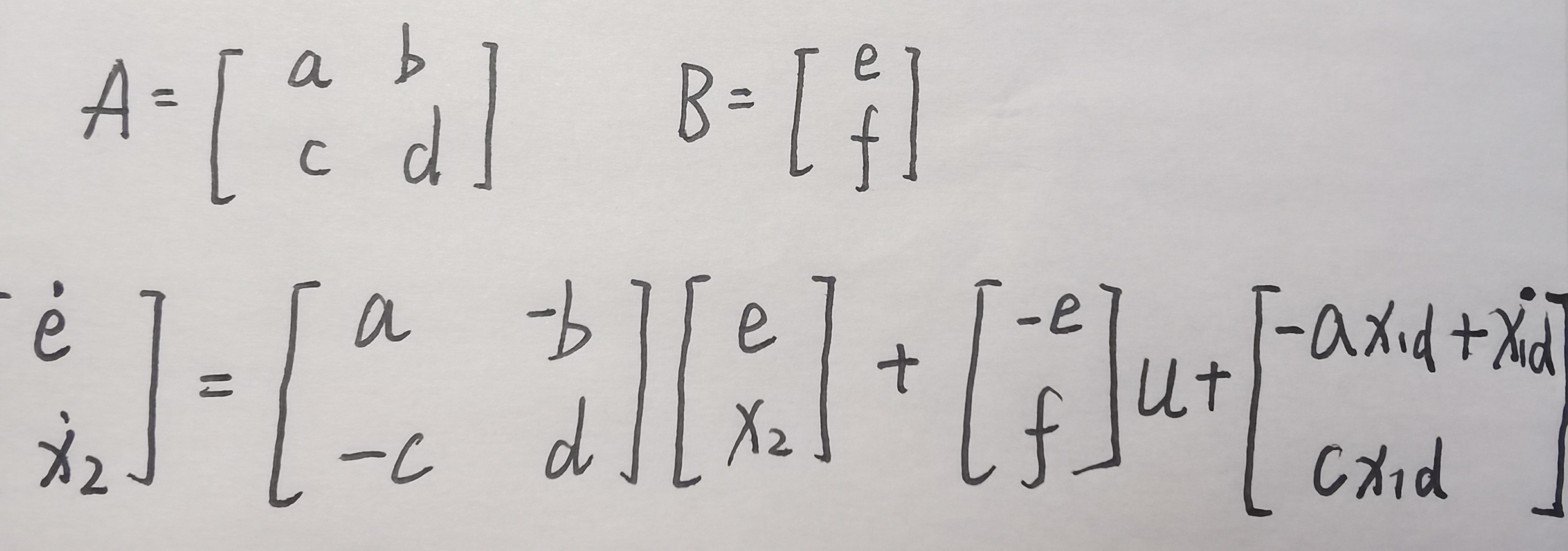
此时,只需要我们调节输入U,使得BU在抵消最后面一个矩阵后还能够做到反馈控制调节系统特征值的作用,就需要U = -kX - a/e*x1d。须注意三点:
- 这里的X是新的包含误差的状态变量;
- 仅有在e、f,a、c成比例,或者对应有0的时候才能完全消去常数,我大胆猜测,这里就对应着经典控制理论中的稳态误差;
- x1ddot这一项的补偿就相当于速度前馈!
这样我们就能够做到轨迹跟踪了!
能观性与观测器
上面内容全部建立在状态向量能够通过传感器测量的前提下,在我们不能够通过传感器获取到一些变量时,我们该如何进行反馈控制?使用观测器!
观测器首先构造一个虚拟的系统进行更新: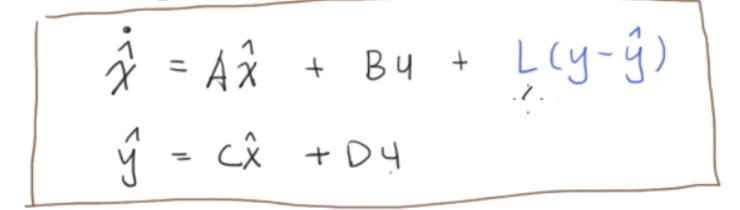
与实际系统做差,可得到如下方程
E_dot = (A-LC)E
其中E = X_hat - X
我们又构造出这样一种形式,同样,只要配置矩阵的特征值,计算出相应的L,即可使E收敛到0,也就是X_hat收敛到X。
这样我们成功观测了状态变量X。
与控制器相同,观测器也需要满足能观性,就是要使L有解,
O = [C CA CA^2 …… CA^n]^T,需要满足O满秩(即Rank = n)
根据分离原理,我们可以使用观测到的值来做状态反馈控制,这样做的时候控制器与观测器特征值不互相影响,仍与原本设计相同!(但我们仍希望能使观测器时间常数小于控制器!)