很早以前就在林哥那儿听过支持向量机这个神奇的名字,是用来识别(分类)装甲板数字的,当时觉得很高深,很硬核。
最近在研读周志华老师所著的《机器学习》,又看到了这个熟悉而又陌生的名词——支持向量机。这次终于能够更深入地了解它了。写此文章来记录。
支持向量机
首先考虑一个二分类问题,我们有一组有标记的样本,分布在样本空间中,假设是一个二维的样本空间,那么它们看起来可能是这样的: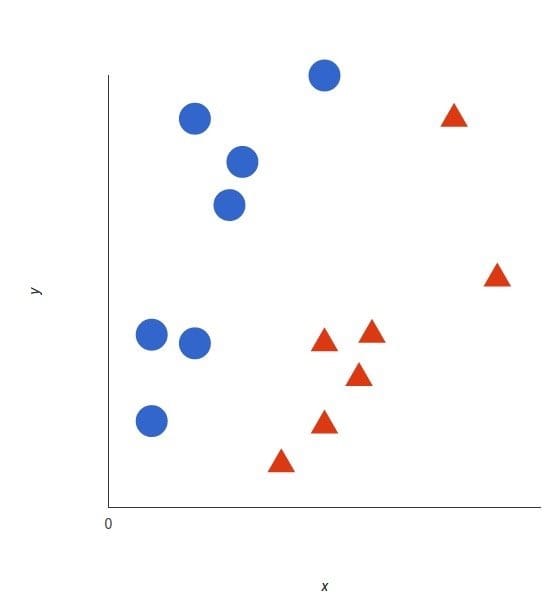
其中我们可以认为三角代表正类而圆圈代表反类。
怎样找到一条直线能够最大程度上地区分正类和反类呢?很容易想到我们需要一条直线(超平面),使它的一侧全是正类,另一侧全是反类。这种情况叫做线性可分的情况,等一会儿我们会讨论基本线性可分与非线性情况。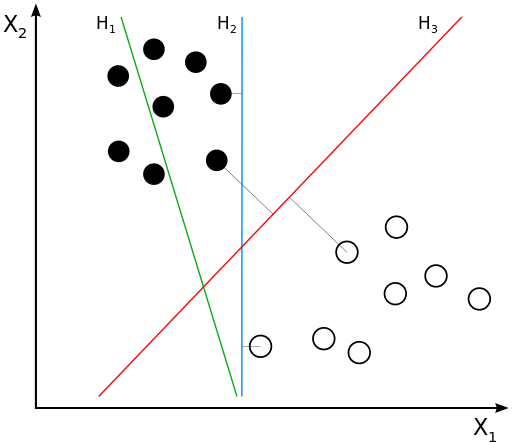
不过这样的直线(超平面)有很多,哪一条更好呢?这里的更好代表着对于新来的样本也能有很好的划分能力,所以我们启发式地想,找一条能够划分样本,并且两边样本到直线最近距离最大且相等的直线。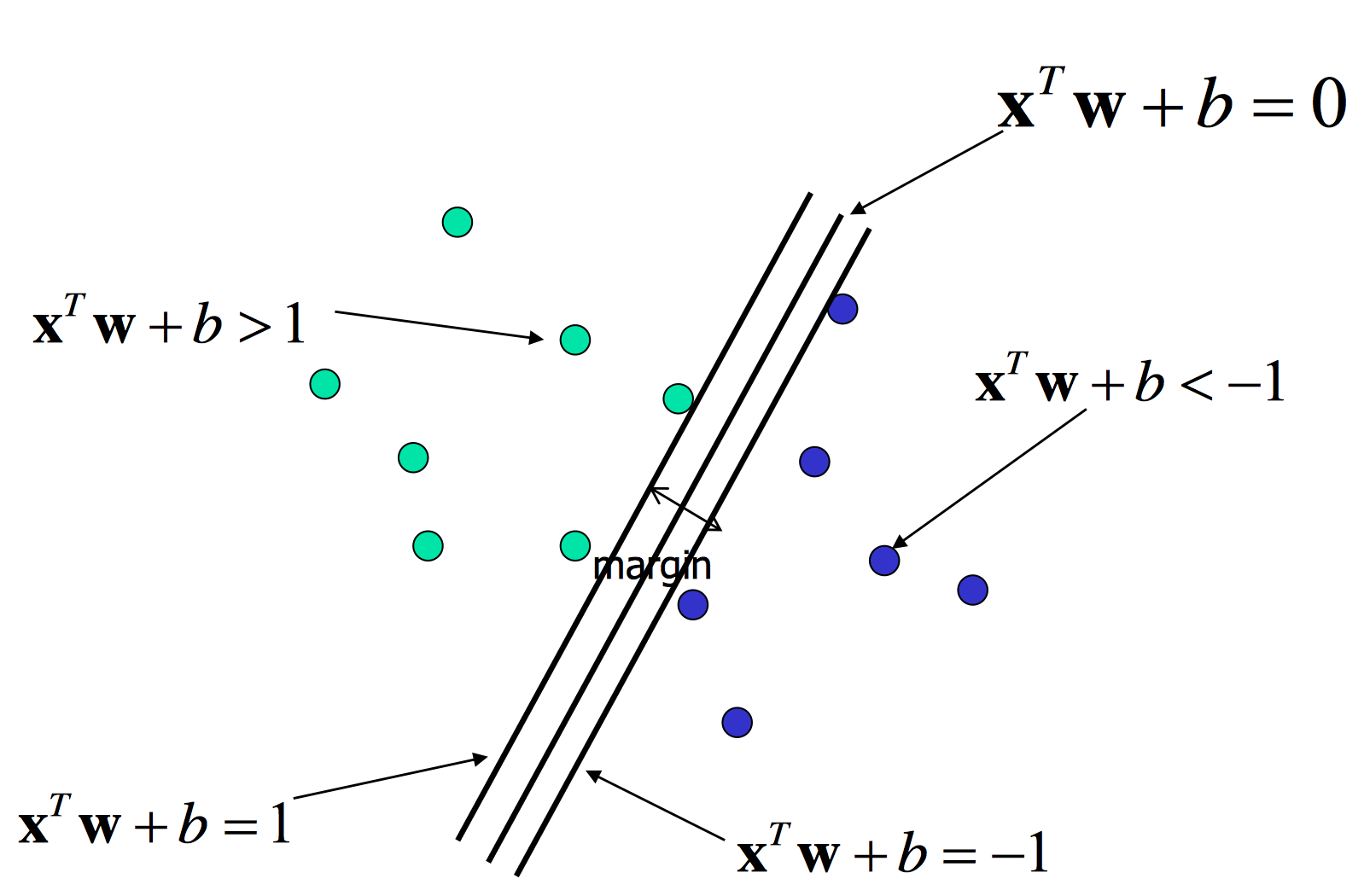
这些据直线最近的样本的位置(向量)就叫做支持向量。
用更严谨的数学表示就是: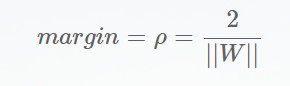
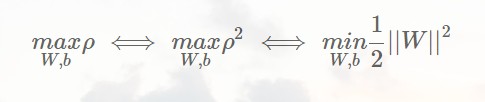
不要忘记我们能够划分样本的条件: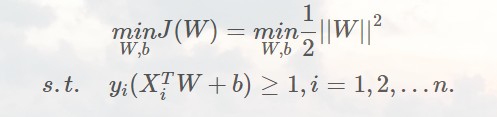
细心的我们可以发现,我们定义的这个直线理应具有dim(w)个自由度,而实际上却有dim(w)+1个参数(别忘了截距b),我们很容易想到,同时放大缩小w与b,直线是不变的,但是对于直线wx+b=1,却是在变化的,因此我们仅仅优化|w|²看似不合理,实际上整条直线已经在条件中进行了限制,所以b也会被考虑进去的。
于是我们使用支持向量机把二分类模型训练问题转化为了一个带不等式约束的优化问题。
我们知道对于等式约束的优化问题我们可以用拉格朗日乘子法进行解决,但是对于不等式约束,我们又该怎样解决呢?
我们称这个优化问题为原始问题,解决办法就是使用拉格朗日乘子法找到一个对偶问题,解决对偶问题并且在满足KKT条件的情况下,我们就能解决原始问题。
那么具体怎么做呢?
首先还是使用拉格朗日乘子法,找到拉格朗日函数: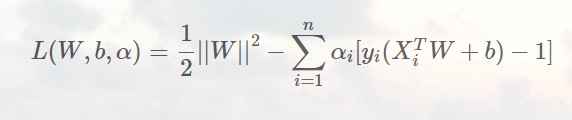
为了把不等式约束消解掉,我们分情况讨论:
如果求得的直线不满足不等式约束,则L取得max只需要α->∞,就有: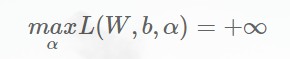
如果满足不等式约束,则有L取得max发生在α=0的情况下,即: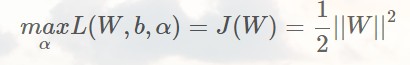
所以我们把不等式约束的优化问题化为双重最值的优化问题: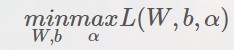
根据对偶原理,它的对偶问题为: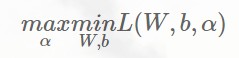
同时还要满足KKT条件: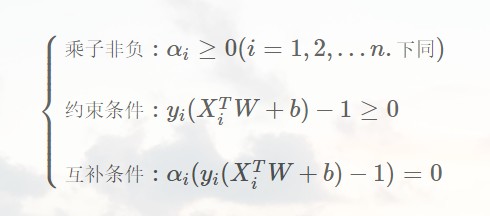
解得最终的超平面为:(具体方法略)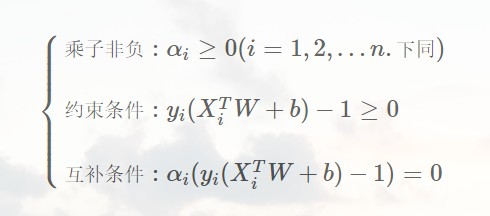
我们还得到一个结论,就是最终发挥作用的样本点只有支持向量,这点我们也能直观地感受到。
还有一些没解决的问题
上面一节我们只讨论了线性可分的情况,如果遇到基本上线性可分的情况(有有限个点被分错),或者非线性可分的情况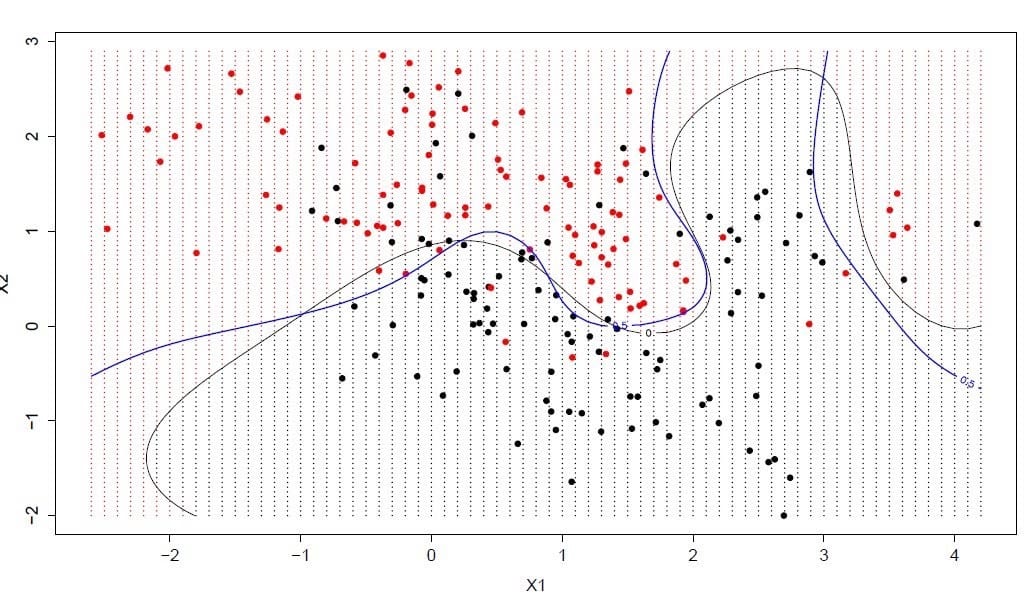
我们该怎么办呢?
1.软间隔法
对于基本上线性可分的情况,我们可以改进优化参数,使其允许一些错误出现,但是要尽最大可能避免这些错误,比如这样: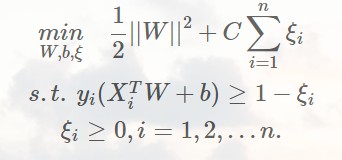
在优化函数中引入惩罚项,惩罚那些超过界限的样本点。
2.核方法
对于非线性的方法,软间隔就不能用了,比如这种情况: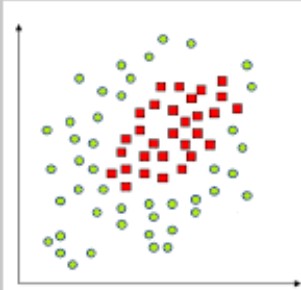
但是我们可以使用一个映射将样本转换到另一个空间中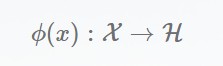
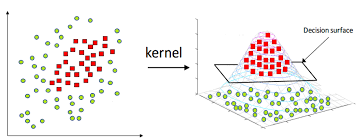
这样就能解决非线性可分的问题了。